rubinghsoftware.de/projects/own

In this page I present a small and simple interpreter for arithmetic expressions in Reverse Polish (RP) notation. It is a general-purpose interpreter, implemented as a C++ library, usable in many different kinds of application programs. The arithmetic, and input and output of numeric values, is done in floating-point numbers exclusively.

The RP interpreter is an extremely small programming project (I completed basic coding in one day, after which I spent two more days on optimization, testing, and code polishing), but despite its simplicity it already demonstrates some of the design elements of interpreters for more complex scripting languages, such as:

Scanning the input text and converting the code to an internal representation that can be executed efficiently, and that stores the information needed to report run-time errors.
Data structures that hold the state of the interpreter machine as visible to and changed by the block of code being executed. (For my RP interpreter: the stack, and the table of variable values.)

The main rationale for including my RP interpreter in this website is lack of time; namely it is a quick way to present on this website a first example of recent C++ source code written by me (until I find the time to complete describing some of the larger and more complex of my own software projects).

VARIABLES, AND IN/OUTPUT

My interpreter extends the basic RP expression idea by the element of named variables. That is, the commands in the expression not only operate on the stack, but also read and write numeric values from and to variables (details in the next section ).

In the RP expression string, the variables are single lower-case letters 'a' ... 'z' (i.e. there are only in total 26 variables available, which is minimal but suffices for simple applications).

These variables are used for the following purposes simultaneously:

Input of numeric values from client code to interpreter;

Output of computed numeric values from interpreter back to client code;

Temporary storage (local variables) during evaluation of the expression.

The variables thus combine the functionality of input variables, output variables, and local variables. The client code determines which of the variable letters are used for input and which for output (as explained here). The remaining variable letters can be used in the expression as temporary variables (these are "local variables" in the sense that their lifetime is limited to the current evaluation of the expression, see below).

Output of computed values to the client code is done via these variables only. In my RP interpreter, there is no notion of a "return value". (This is in contrast to usual RP expressions, which leave one element on stack at the end of the expression, and then return that value.) [1]
As a consequence, as a strict rule my interpreter accepts only expressions that leave the stack exactly empty at the end of the expression. Making the stack empty is very naturally done by the operation that pops a value from stack and copies it into a variable (see next section ).

SYNTAX OF THE RP EXPRESSION STRING

The interpreter receives as input a string containing the RP expression. This string contains a sequence of lexical elements, processed in order from left to right. Space characters are allowed between lexical elements (but tab or newline characters are not allowed).

A lexical element can be one of the following:

A single lower-case letter 'a'...'z' not preceded by an equals sign means push the value of the variable onto stack.

A single lower-case letter preceded by an equals sign "=a" ... "=z" means pop a value from stack and copy it into the variable. Note that the equals sign is treated as an integral part of the variable name, and is not an operator character. There can be no space between the '=' and the variable letter.

A decimal floating-point number without sign (e.g. 2, 0.25, .5) means push this nonnegative constant value onto stack.

Arithmetic operators: There are only binary operators, namely

`'+'`	Add
`'-'`	Subtract	(`ab-` means `a - b`)
`'*'`	Multiply
`'/'`	Divide	(`ab/` means `a / b`)
`'^'`	Exponentiate	(`ab^` means `a^b`)

Each of these pops two values from stack, computes, and pushes the result.

At character ';' the interpreter checks whether the stack is empty at that point, and generates an error if this is not the case. Stack and variables are left unchanged.

The items with the yellow bullets () are my own extensions to basic RP syntax.

The ';' operation is completely optional. It is an optional validation check (like an assertion in C/C++) available to the person who codes the expression. Its usefulness is that with it you can use the interpreter to help detect coding errors (i.e. logical errors) in complex expresssions. Put this in in a complex expression at the points where by design the stack should be empty (often the case after writing a value to a variable).
The stack state is of course the one big main thing that determines the correctness of a RP expression, and stack emptyness is a simple but very useful test. The usefulness arises because with the ';' you can cut up a long expression into chunks, each of which is a valid and complete RP expression on its own (as verified by the interpreter). This very greatly localizes coding errors, and thereby is a significant help in coding a complex RP expression string.

At the end of the expression, the interpreter always executes the empty-stack test automatically (therefore a ';' at the very end of the expression is redundant).

Examples of expression strings accepted by my interpreter:

a.3* b.7* + =z Compute 0.3 a + 0.7 b, and copy the result into the variable z.
.3=f ; fa* 1f-b* + =z Set the temporary variable f to the value 0.3, and check that the stack is empty. Then compute f·a + (1-f)·b and copy the result into the variable z.

USAGE BY CLIENT CODE

An application typically reads a RP expression only once, and then evaluates the expression many times on different values of the input variables.

The following application code fragment instantiates an interpreter object, and then reads the 0-terminated expression string in the char const * variable arg_expr into the interpreter object. The 'scanFromString()' call parses the string and converts the expression to a representation (stored inside the rp object) that can be executed efficiently.

 #include "rpinterpreter.h" 

 // Instantiate interpreter object.
 RPInterpreter rp;
 
 // Read expression.
 if ( ! rp.scanFromString( arg_expr ) ) { /*Error in expression*/ }

The following application code fragment evaluates the expression, given the values of the input variables 'a', 'b', 'c' as determined by the application code. (The variables not used as input variables are cleared to zero; this is explained in the next section.) After expression evaluation, the code fragment then reads the values of the two output variables 'x' and 'y'.

 // Clear all variables to zero.
 rp.clearVars();

 // Set input variables.
 double aIn = ...;
 double bIn = ...;
 double cIn = ...;
 rp.putVar( 'a', aIn );
 rp.putVar( 'b', bIn );
 rp.putVar( 'c', cIn );
 
 // Evaluate expression.
 rp.evaluate();
 
 // Get values of output variables.
 double xResult;
 double yResult;
 if ( ! rp.getVar( 'x', &xResult ) ) { /*Domain error FPE in computation of x*/ }
 if ( ! rp.getVar( 'y', &yResult ) ) { /*Domain error FPE in computation of y*/ }

The application determines which of the variables (variable letters) are input variables simply by means of setting the values of these variables prior to the evaluate() call. And it determines which of the variables (variable letters) are output variables simply by means of reading the values of these variables after the evaluate() call.
Which variables (variable letters) are used as input, which as output, and which as both input and output is therefore fixed by the application code (and not by the RP expression). In typical application programs, the number of input and output variables and their names would simply be hardcoded, as in the code fragment above.[2]
The person who writes the RP expressions that are passed to the application program of course has to know which variable letters are used as input variables and which as output variables. This information should be specified in the interface/usage documentation of the application program.

"LOCAL" AND "GLOBAL" VARIABLES

In the last application code fragment above, the variables not used as input variables are cleared to zero (by the clearVars() call) before the expression is evaluated. This is what application code should normally always do.

Clearing the variables that are not used as input variables to zero creates a clean evaluation environment for the expression. But more importantly and very much more fundamentally, it has the effect of making the variables not used as either input or output variables into "local variables" in the sense that their lifetime is limited to one single evaluation of the expression. In other words, the values of these variables do not carry over from one evaluation of the expression to the next evaluation of the same expression. This limited lifetime is what most applications would normally want.

Leaving out the clearVars() call would have the effect that the values of the variables not used as input variables (= the variables not set in the application code via the putVar() calls) then become "global variables" (and also "static" variables in C/C++ terminology) in the sense that their values carry over from one evaluation of the expression to the next evaluation of the same expression.

The application code determines whether the variables that are neither input nor output variables are "local" or "global". (And it can even make only a subset of them into "locals", by calling putVar(...,0) on that subset.) In other words, the application code is responsible for ensuring that the non-input-non-output variables become local variables (if that is the behaviour that is desired), by making the the clearVars() call.

INTERPRETER DESIGN

Separation of lexical analysis and parsing from execution

For very simple script languages (like the RP notation) it would be in principle possible to execute the script supplied by the user immediately from the script text, i.e. to combine lexical analysis, parsing, and execution into one combined operation.

However, when the interpreter should be usable in applications in which the same script (RP expression) is executed many times (each time on different inputs), then it is much better to use the approach of first converting the script text (the RP expression) into an internal representation, that is then executed at a later time. The design of this internal representation is chosen so that it can be executed efficiently.

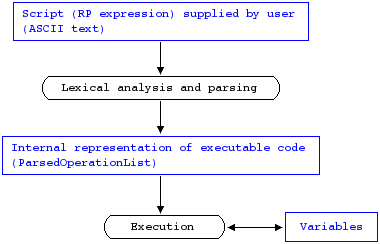
(Fig. 1) Data flow diagram. The RP expression text is first converted into an internal representation (ParsedOperationList) which can be executed later.
During execution, this internal representation of the RP expression is read-only, whereas the variables are read+write.

This approach separates on the one side lexical analysis and parsing, from on the other side the execution. In this way, lexical analysis and parsing do not have to be repeated over and over each time the expression is executed, which of course makes execution extremely much faster. This is the approach followed in my RP interpreter.

ParsedOperationList

The RP expression is simply an ordered list of operations, where each operation is the operation belonging to one of the lexical elements described in the syntax section above. I store the parsed RP expression simply in the form of an ordered list of these operations:

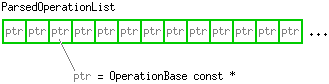
(Fig. 2) The class ParsedOperationList, which contains the parsed RP expression. It is an ordered list of const pointers to OperationXxx objects, each of which specifies one operation. Execution consists of evaluating these OperationXxx objects in order.

Each operation is implemented as a subclass of the abstract base class OperationBase. The abstract base class defines the pure virtual function execute(). In each subclass, this function is implemented to execute the operation, given the stack and the variables.

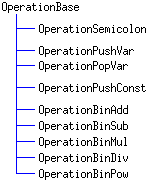
(Fig. 3) Class hierarchy of the OperationXxx classes. Each implementation class defines one of the operations in the RP expression.
The implementation classes OperationPushVar, OperationPopVar, OperationPushConst have a constructor argument that specifies the name of the variable or the constant numerical value that is being pushed/popped. The value of the parameter is stored in the implementation class as a constant instance variable.

Objects of the OperationXxx implementation classes are created during the lexical analysis and parsing stage, and are thereafter never changed; the ParsedOperationList therefore contains const pointers to these OperationXxx objects.

In order to make the evaluation of the parsed RP expression as fast as possible, each of the arithmetic operations OperationBinXxx is coded out as separate OperationBase subclass. A perhaps more "elegant" object-oriented design would have been to make one combined class for all the binary operations, which is passed a parameter defining the exact arithmetic operation to be executed — however this would have meant one additional level of indirection, which comes with an execution speed price.
The level of indirection that is already there (the pure virtual base class OperationBase) is the minimum required to realize the functionality. (And implementing that indirection via the virtual base class method —i.e. by using function pointers— is the fastest possible way.)

A further speed optimization that was made, is to make the implementation of the execute() function in each of the OperationXxx implementation classes as streamlined as possible. The stack operations, and the operations to read and write the value of a variable, are all implemented as inline functions. Furthermore, in the implementation of the execute() function for the OperationBinXxx classes, no checking is done for floating-point exceptions (FPEs) occurring in the arithmetic operation being executed, as explained in the section Floating-point exceptions above.

Execution speed is important for applications like the image filter program, in which the same RP expression is evaluated very many times. Together, the speed optimization measures mentioned above almost double the speed of the execution of a parsed RP expression.

SContext and internal exceptions

An interesting problem in coding an interpreter is error messages. When an eror occurs during the execution of a script (RP expression), then a sensible interpreter implementation should give in its error message to the user the information exactly where in the input script (character number in the RP expression string) the operation is located where the error occurred, so that the user is enabled to find the offending location in the script.
This means that the internal representation of the parsed script, i.e. the representation of the script that is executed by the interpreter, should contain for each lexical element (token) that leads to an item in the executable representation also the information exactly where in the input script that element was found.

In my RP interpreter, I solved this as follows. During lexical analysis and parsing, the current read position in the input expression is kept updated in an object of class SContext (Scanning Context). A copy of this SContext object is passed as a constructor argument to each OperationXxx instance that is created, in which it is stored as a constant instance variable. At an execution error (such as stack under/overflow), an exception of the internal exception type Ex is thrown; this exception object gets passed as a constructor argument the SContext object stored in the OperationXxx instance currently being executed.

As an aspect of isolating the implementation from the interface exported to the client code, all exceptions are caught interally by the member functions of the client-used class RPInterpreter, so that these internal exceptions (and the definition of the internal exception class Ex) are not passed on to the client code.

Trial execution

As a measure to report possible execution errors to the client code as quickly as possible, the exported function RPInterpreter::scanFromString() which reads the input expression string and converts it to the internal ParsedOperationList representation, also executes one single trial evaluation of the parsed expression: This single trial evaluation catches all possible stack under- and overflow errors.
As a result, the only possible remaining remaining run-time error during a call of the exported function RPInterpreter::evaluate() by the client code, is the floating-point domain error. These domain errors do not cause internal Ex exceptions, but result in NaN values of the output variables (which are checked for by the RPInterpreter::getVar() function).

Interpreter state

During the execution of the RP expression, the ParsedOperationList is read-only information. The set of data that changes during the execution of the RP expression is the following:

The stack. The items on the stack are floating-point numerical values. The stack is local to every individual evaluation of the expression, and is a local variable inside the internal function evaluateRPExpression() which implements the exported RPInterpreter::evaluate() function.
The variables. Since the variables are not only used as local variables, but are used also to pass input and output values to and from the client code, the variable values must be preserved between calls to the RPInterpreter member functions (specifically, between putVar(), evaluate(), and getVar()). Therefore, the table of variable values (VarTable) is a member variable of the class RPInterpreter.

Isolation of the implementation

One of the ugly aspects of C++ is that there is no way to leave out the private part of a class from the class declaration published to client code. As a result, the header file in which a class is declared that is used by client code gives the client code access to all the internal data types that are used in that class declation.

In the the class RPInterpreter, which is the only class exported to the client code, I make use of a well-known trick to circumvent this limitation of C++, and to achieve in spite of it that all internals of the class are hidden from the client code. The trick is that the class contains as member variables only void pointers:

 class RPInterpreter
 {
 	void * m_exprdata; //Parsed expression data. Implementation is hidden.
 	void * m_vardata;  //Values of the variables. Implementation is hidden.
 
 public:
 	...
 };

In the implementation of the RPInterpreter constructor, these two void pointers are initialized to point to newly allocated instances of the two implementation classes (ParsedOperationList and VarTable, respectively) in which the actual data is stored. And in the implementation of the RPInterpreter member functions, to access this data, the two void pointers are cast to pointers to these two implementation classes, respectively.

In this way, the implementation classes (ParsedOperationList and VarTable) do not have to be published to client code. The casting is the thing that cuts the datatype declaration dependency, which in turn allows the implementation data types to be kept hidden from the client code. As a result, the header file rpinterpreter.h (which is the only header file exported to and included by client code) is kept very clean and does not reveal any internals of the implementation. [3] [4]

FLOATING-POINT EXCEPTIONS

Introduction

In my RP interpreter, the arithmetic, and the input and output of numeric values from and to the client code, is done in floating-point numbers exclusively (C/C++ built-in data type double).

In arithmetic operations on floating-point numbers, situations can occur in which the result of the operation is either undefined or can not be represented as a regular floating-point number. The technical term for such a situation is: Floating-Point Exception, abbreviated FPE.[5]

I used this project to experiment with a simple and slightly unusual (but completely logical and practical) way to handle FPEs. Namely: The approach is that during the evaluation of the RP expression, only the occurrence of FPEs of the type domain error is checked for and reported to the client code. The rationale behind this is that the domain error is the only kind of FPE that means that there is a logical error in the RP expression. For arithmetic operations in which any other kind of FPE occurs, the interpreter silently uses a sensible approximate result value.

Domain error, and the other kinds of FPE

A domain error means that the arithmetic operation is undefined for the values of the operands. Examples are: dividing zero by zero; and raising a negative number to a negative noninteger exponent. "Operation undefined" means that the operation is mathematically illegal for these operands, and that there does not exist a value for the result of the operation, not even theoretically.

The domain error is the gravest kind of FPE. When a domain error occurs, this means that there is a logical error in the mathematics.

For each of the other possible kinds of FPE (underflow, overflow, pole error, see Table 1 below), the problem is not that the operation is mathematically undefined or that (from the point of view of theoretical mathematics) there is a logical error in the mathematics; instead, these other FPEs mean only that the result can not be represented exactly given the finiteness of the actual number representation format. In these cases, it is still possible to set the result to an approximate value that is meaningful to the client code.
The approximate result values that we use in case of any of these other kinds of FPE are shown in Table 1 (column "Default return value"). The meaning of "infinity" is explained below. The value zero is of course entirely unproblematic. That it is easy in actual practice for client code to process the ± infinity values in the same way as normal, finite result values is demonstrated here.

(Table 1) Floating-point exceptions (FPEs), and their IEEE 754-2008 flags and default return values. The "Flag" column specifies the symbolic flag value from the C/C++ library interfaced by <fenv.h>.

FPE	Flag	Default return value
Domain error, also called Invalid operation error. This means that an operation was executed on operand values that lie outside of the intervals for which the operation is defined, for example raising a negative number to a negative noninteger exponent.	`FE_INVALID`	NaN
Pole error, also called DivideByZero error. This category is wider than the name DivideByZero implies. It includes not only the division of a nonzero number by zero, but also any other operation that logically gives a result of plus or minus infinity, such as log(0). (By the way, note that dividing zero by zero is a domain error, not a pole error.)	`FE_DIVBYZERO`	+ or - infinity
Overflow. This means that the result is finite but too large in absolute value to be represented in the floating-point number format.	`FE_OVERFLOW`	+ or - infinity
Underflow. This means that the result is larger than zero in absolute value but too small to be represented in the floating-point number format.	`FE_UNDERFLOW`	0 (zero)

IEEE 754-2008 default handling

The FPE handling in my RP interpreter is built upon the IEEE 754-2008 standard for floating-point arithmetic.[6] Virtually all modern hardware platforms and programming languages (including C/C++) conform to this standard.

More specifically, the FPE handling in my RP interpreter is built upon the so-called default handling defined inside IEEE 754-2008. This default handling is the handling that IEEE 754-2008 specifies to happen by default when no special configurations are made. It is what is used in 99.9% of all numerical software.

This default handling is extremely simple, namely: When an operation is executed in which a FPE occurs, then a flag[7] is set (which tells which kind of FPE occurred), and then processing is simply continued, using one of a set of special values (see Table 1) for the value of the result of the operation.

NaN and infinity

Every IEEE 754-2008 floating-point number — such as an instance of the C/C++ built-in datatype double — can contain not only a regular numerical value, but can instead also contain one of the special symbolic values NaN ("Not a Number") and infinity; both of these are signed.

Under IEEE 754-2008 default handling, these special values can be returned as the result value of an arithmetic operation, in case of a FPE. Furthermore, IEEE 754-2008 also guarantees that each of these special values is always accepted as the value of one or more of the input operands in any arithmetic operation, giving the result one would logically expect (for example, adding plus infinity to any finite number gives plus infinity as the sum).

NaN is is associated with, and only with, the domain error FPE. In IEEE 754-2008 default handling, it is the return value used for an arithmetic operation in which a domain error occurs.
An essential aspect of NaN is that it propagates: this means that every floating-point operation on operands one or more of which is a NaN, returns NaN as the result of that operation.
The values of plus infinity or minus infinity, with the sign set to that of the theoretical infinite-precision result, are in IEEE 754-2008 default handling returned in case of a pole error and also in case of an overflow error.
A notable feature of these infinity values is that they are ordered with respect to any finite floating point number in the expected way (i.e. minus infinity is smaller than any finite number, and plus infinity is larger than any finite number). As a consequence, the floating-point comparison operations (a < b, a <= b, a > b, a >= b) give the expected result when used to compare these + or - infinity values against finite floating-point numbers.

FPE handling design of the RP interpreter

The FPE handling approach followed in my RP interpreter is the same as the approach behind the IEEE 754-2008 default handling. Namely, on occurrence of a FPE, the evaluation of a RP expression is never prematurely aborted. Instead, the approach is followed to let all computations (that were initiated by the client code) run to completion, and then to check afterward whether during those computations any FPE occurred.
When any kind of FPE happens in an arithmetic operation during the evaluation of an expression, the interpreter simply uses the IEEE 754-2008 default handling: i.e., the floating-point flag is set; the result of the operation is set according to Table 1; and processing is continued.

As consequence of this, the special values NaN and infinity (signed) can occur as the value of any output variable. However, these two special values of output variables have a very different meaning for the client code (application code) using the RP interpreter library:

NaN occurs as the value of an output variable if and only if there was a domain error in the computations of the value of that output variable. Thus, NaN indicates a logical error in the combination of the RP expression plus the values of the input variables. For this output variable, no value is available.
Because of this, a NaN-valued output variable would (should) normally not be processed further by the application software; instead, the application software would in this case normally abort with an error message to the user.
(Note: To make it easy for the application software to detect this error condition, the getVar() function used in the client code to retrieve the value of an output variable returns false if and only if the output variable has a NaN value.)
Plus or minus infinity: In the design philosophy of the RP interpreter, ± infinity are regarded as completely regular values for an output variable, and not as indications of an error condition.
These ± infinity values for the output variables are unproblematic for the typical application program; and in the typical application program, these ± infinity values can be processed by the same processing path as the one through which finite values of the output variables are passed. This is demonstrated below.
The typical client code (that uses the RP interpreter library) would normally always pass the every value of each of the retrieved output variables through a clipping function (as shown below), to limit the value to the interval that is relevant to the application. Examples: the Function Plotter example application restricts the output variable value to the range of the Y axis; and the Image filter" example application restricts each of the output variable values to the range [0.0, 1.0] of a color coordinate.
double clip( double iVal ) { if ( iVal < MYMIN ) { return MYMIN; } if ( iVal > MYMAX ) { return MYMAX; } return iVal; }
Because of the ordering property of the ± infinity values relative to finite values, iVal values of ± infinity are automatically handled correctly by the the clipping function above. (MYMIN and MYMAX are any finite real numbers.) Thus, we see that the application code handles the ± infinity values completely regularly.

FPE checking resolution

As explained above, IEEE 754-2008 default handling is not interrupt-based, but is based on polling (of the flag) by the application code: that means, the application code must expend running time to check whether FPEs occurred (by checking the flag).
The IEEE 754-2008 default handling is therefore clearly designed to be used with a FPE checking approach with a "resolution" that is less detailed than individual floating-point operations. — That is, for application code in which not every individual floating-point operation is checked for the occurrence of a FPE (which would add proportionally rather much to the running-time cost of each floating-point operation), but rather where it suffices that it is detected whether a FPE occurred anywhere during a longer sequences of floating-point operations.

In my RP interpreter, each individual arithmetic operation in the RP expression is executed by one of the OperationBinXxx::execute() functions.
It would have been possible, of course, to add into the body of each of these functions the feclearexcept() and fetestexcept() calls[7] necessary to check for occurrence of an FPE in that single operation. This would have produced the most detailed FPE checking resolution possible — but at the cost of making these execute() functions (and therefore the whole execution of a RP expression) significantly slower.
Instead, I preferred implementing the interpreter it so that it achieves the maximum possible execution speed, above implementing it so that it achieves the maximum possible FPE reporting resolution. Therefore, I left all FPE checking code out of the execute() functions — thus achieving the best possible execution speed, at the cost of less detailed FPE checking.

Checking for domain error

There are two possible ways to check for the occurrence of a domain error in a sequence of arithmetic operations: [8]

Bracketing the sequence between feclearexcept() and fetestexcept() calls[7], to check the floating-point flag. This method of course works for any kind of FPE, not only for the domain error.
Checking whether one of more of the output values of the sequence has the value NaN. This method is possible only for the domain error (which is the only FPE returning NaN), and relies on the propagation property of NaN.
The effect of this propagation behaviour is that when a domain error occurs in a long chain of arithmetic operations (a chain such that the output of one operation is used as the input of the next), that the occurrence of a domain error in any operation in this chain is guaranteed to lead to a NaN in the final result.

Internally in the interpreter, the first method, flag-polling, is never used. The client code of the RP interpreter library is however still free to bracket evaluations of the RP expression (i.e. evaluate calls, or whole sequences of evaluate calls) between calls to the functions feclearexcept() and fetestexcept().

The only domain error checking performed inside the RP interpreter library is based on the second method, checking for NaN. Namely, the function getVar(), which is the function which client code retrieves the value of a variable, uses a return value that is false when the value is NaN (meaning that a domain error occurred in the chain of arithmetic operations leading to the value of the variable), and true otherwise (meaning that no domain error occurred).

(Note: This checking for a NaN value could of course in principle have been left to the client code. I added the getVar() return value feature as a convienience to client code, so that as the client programmer does not have to look up how to check a double number for NaN. This also helps hide away more of the "nuts and bolts" of the underlying number representation inside the RP library, keeping these low-level details out of the client code.)

Checking for other FPEs

My RP interpreter internally does not check for any other kind of FPE than the domain error. As explained above, my expectation is that the typical application program would be able to handle the ± infinity output variable values via the same processing pipeline as normal, finite output variable values; and therefore, that it would typically not be not necessary for application programs to detect other kinds of FPE than the domain error.
However, application code (client code of the RP interpreter library) is still free to check for other FPEs than the domain error occurring during RP expression evaluations; it can do so by means of bracketing these evaluations between calls to the functions feclearexcept() and fetestexcept().

FPE handling usage in the client code

To check for the occurrence of domain error FPEs, the client code can do one (or both) of the following two things:

Check the return value of every call of the function getVar(). This gives the most fine-grained domain error checking that is possible with the RP interpreter library.

 // Set input variables.
 ... 
 
 // Evaluate expression.
 rp.evaluate();
 
 // Get values of output variables.
 double xResult;
 double yResult;
 if ( ! rp.getVar( 'x', &xResult ) ) { /*Domain error in computation of x*/ }
 if ( ! rp.getVar( 'y', &yResult ) ) { /*Domain error in computation of y*/ }

(For an example showing this approach being used in actual code: see the function filterPixel() in fltrppm4.cpp.)

— and/or —

Bracket a sequence of sequence of one or more RP expression evaluations between calls to feclearexcept() and fetestexcept().

 // Clear the floating-point flag.
 feclearexcept( FE_ALL_EXCEPT );
 
 // Run rp.evaluate() multiple times on different input variable values.
 ...
 
 // Test floating-point flag for domain error.
 if ( fetestexcept( FE_INVALID ) ) { /*Domain error in any of the evaluations*/ }

(For an example showing this approach being used in actual code: see the main() function in fltrppm4.cpp.)

The variable rp in the two code snippets above is an object of the class RPInterpreter, instantiated in the client code (see the example in the section Usage by client code).

SOURCE CODE

The RP expression interpreter is implemented as a C++ library. The only header file that is published to the client code using the library is rpinterpreter.h.
The only external dependencies of the source code are the standard C libraries interfaced by the header files <assert.h>, <stdio.h>, and <math.h>.
Coding style: Consistently throughout all source files, I use my new notation scheme for function parameters, with one-character prefixes that specify not datatypes but the direction of information flow.

Internal dependency structure

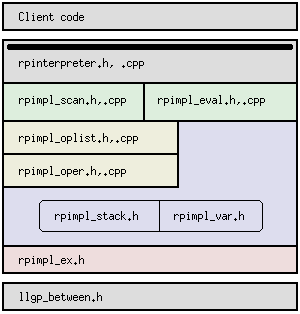
(Fig. 4) Dependency diagram. A block uses only the blocks strictly vertically below it.
The thick horizontal line inside the rpinterpreter.h,.cpp block means that this block isolates all blocks below it from the blocks above it.
Blocks without such a thick horizontal line in them are "permeable", that is: they pass on their own dependencies to the blocks above them.

Listing of the source files

`rpinterpreter.h` `rpinterpreter.cpp`	The class `RPInterpreter`. This is the only class exported to the client code.
`rpimpl_scan.h` `rpimpl_scan.cpp`	Internal function `evalRPExpression()` — Scan a RP expression string and convert it into a `ParsedOperationList` (which is a list of `OperationXxx` instances).
`rpimpl_eval.h` `rpimpl_eval.cpp`	Internal function `evaluateRPExpression()` — Evaluate `ParsedOperationList` (read-only), using a given `VarTable` instance (read + write) for the variables.
`rpimpl_oplist.h` `rpimpl_oplist.cpp`	Internal class `ParsedOperationList` — Ordered list of `OperationXxx` instances. Contains a parsed RP expression.
`rpimpl_oper.h` `rpimpl_oper.cpp`	The internal `OperationXxx` classes — Each `OperationXxx` instance executes a specific operation (changing stack and variables) during the evaluation of a RP expression.
`rpimpl_stack.h`	Internal class `StackDbl` — Stack of `double` values, used for the evaluation of a RP expression. All its member functions are defined as inline functions.
`rpimpl_var.h`	Internal class `VarTable` — List of the variables (each of type `double`), used for the evaluation of a RP expression. All its member functions are defined as inline functions.
`rpimpl_ex.h`	Internal exception class and scanning context class (character number in input string).

`llgp_between.h`	General-purpose macros `BETWEEN_IE()` and `BETWEEN_II()`, which test whether a number falls inside an interval: min ≤ x < max, or min ≤ x ≤ max. »more

The source directory contains also the following documentation file:

rpinterpreter_doc_floatingPointErrors.txt Text file documenting how the interpreter handles floating-point exceptions (FPEs) in the arithmetic operations in the RP expression.

The links above lead to representations of the source files in the form of HTML pages. (Done in this way to make it possible to view the sources in a webbrowser.)
A gzip archive that contains all source files in their original form (and with the original file names) is here. Unpack: gunzip rpinterpreter.tar.gz, then tar -xvf rpinterpreter.tar

Build

Because the design presupposes that all floating-point arithmetic operations are executed according to the default handling defined in IEEE 754-2008, it is essential that a compiler (and compiler options) are used that creates code in which this IEEE 754-2008 default handling is used for the floating-point operations. For example, with the GNU gcc compiler, the option -funsafe-math-optimizations should not be used.

On GNU/Linux, the following commands build the sources to the static library rpinterpreter.a :

  g++              -ggdb -Wall  -c rpimpl_oper.cpp
  g++              -ggdb -Wall  -c rpimpl_oplist.cpp
  g++  -std=c++0x  -ggdb -Wall  -c rpimpl_scan.cpp
  g++              -ggdb -Wall  -c rpimpl_eval.cpp
  g++              -ggdb -Wall  -c rpinterpreter.cpp
  
  ar rcs rpinterpreter.a  \
        rpimpl_oplist.o rpimpl_scan.o rpimpl_eval.o rpinterpreter.o

The compiler option -std=c++0x is for the C++11 feature static_assert(), used in rpimpl_scan.cpp. The gzip archive mentioned below the source listing contains a UNIX shell script build_rpinterpreter.sh that executes the above commands for compilation and for creation of the static library file.

EXAMPLE APPLICATION PROGRAMS

This section gives three example application programs for the RPInterpreter library. Each of these three application programs is implemented as a single C++ source file. [9]

Test driver

Source file: testrp4.cpp

This is a minimalistic main() for testing the RPInterpreter class. The program reads in the RP expression string specified as the command-line argument, and then evaluates the expression one single time (and only one single time), on variables with hardcoded input values (namely, the variables a, b, c have fixed nonzero input values, and all others have zero input values). After the evaluation of the expression, the program prints the values of all variables to stdout.

Function plotter

Source file: plot4.cpp

This simple application prints to stdout a crude ASCII plot of y as a function of x, as defined by the Reverse Polish expession specified as the command-line argument. In the RP expression, x is the input variable and y is the output variable. All other variable letters are local variables.
The plot ranges over x = 0.0 to x = 1.0, in a fixed number of steps; and the plotted y range is [0.0, 1.0]. These ranges are fixed.[10]

Example: The command

   ./plot4 'x2* .3- 2^ =y'

defines the function y(x) = (2x - 0.3)², and prints the following plot to stdout:

 x=+0.000e+00 y=+9.000e-02    |     *                                                          |  
 x=+2.500e-02 y=+6.250e-02    |   *                                                            |  
 x=+5.000e-02 y=+4.000e-02    |  *                                                             |  
 x=+7.500e-02 y=+2.250e-02    |*                                                               |  
 x=+1.000e-01 y=+1.000e-02    |*                                                               |  
 x=+1.250e-01 y=+2.500e-03    *                                                                |  
 x=+1.500e-01 y=+0.000e+00    *                                                                |  
 x=+1.750e-01 y=+2.500e-03    *                                                                |  
 x=+2.000e-01 y=+1.000e-02    |*                                                               |  
 x=+2.250e-01 y=+2.250e-02    |*                                                               |  
 x=+2.500e-01 y=+4.000e-02    |  *                                                             |  
 x=+2.750e-01 y=+6.250e-02    |   *                                                            |  
 x=+3.000e-01 y=+9.000e-02    |     *                                                          |  
 x=+3.250e-01 y=+1.225e-01    |       *                                                        |  
 x=+3.500e-01 y=+1.600e-01    |         *                                                      |  
 x=+3.750e-01 y=+2.025e-01    |            *                                                   |  
 x=+4.000e-01 y=+2.500e-01    |               *                                                |  
 x=+4.250e-01 y=+3.025e-01    |                   *                                            |  
 x=+4.500e-01 y=+3.600e-01    |                      *                                         |  
 x=+4.750e-01 y=+4.225e-01    |                          *                                     |  
 x=+5.000e-01 y=+4.900e-01    |                               *                                |  
 x=+5.250e-01 y=+5.625e-01    |                                    *                           |  
 x=+5.500e-01 y=+6.400e-01    |                                         *                      |  
 x=+5.750e-01 y=+7.225e-01    |                                              *                 |  
 x=+6.000e-01 y=+8.100e-01    |                                                    *           |  
 x=+6.250e-01 y=+9.025e-01    |                                                          *     |  
 x=+6.500e-01 y=+1.000e+00    |                                                                *  
 x=+6.750e-01 y=+1.103e+00    |                                                                | >
 x=+7.000e-01 y=+1.210e+00    |                                                                | >
 x=+7.250e-01 y=+1.323e+00    |                                                                | >
 x=+7.500e-01 y=+1.440e+00    |                                                                | >
 x=+7.750e-01 y=+1.563e+00    |                                                                | >
 x=+8.000e-01 y=+1.690e+00    |                                                                | >
 x=+8.250e-01 y=+1.823e+00    |                                                                | >
 x=+8.500e-01 y=+1.960e+00    |                                                                | >
 x=+8.750e-01 y=+2.103e+00    |                                                                | >
 x=+9.000e-01 y=+2.250e+00    |                                                                | >
 x=+9.250e-01 y=+2.403e+00    |                                                                | >
 x=+9.500e-01 y=+2.560e+00    |                                                                | >
 x=+9.750e-01 y=+2.723e+00    |                                                                | >
 x=+1.000e+00 y=+2.890e+00    |                                                                | >

The x-axis points vertically downward, and the y-axis points horizontally to the right. Each line of the output corresponds to an x value for which the expression was evaluated. At the left of each line, the numeric values of the input x and the output y are printed for that evaluation.
The y values are plotted in the range [0.0, 1.0]. The pipe character on the left corresponds to y = 0.0, and the pipe character on the right corresponds to y = 1.0. When y is below 0.0, then a '<' character is printed in the left margin; and when y is above 1.0, then a '>' character is printed in the right margin.

Image filter program

Source file: fltrppm4.cpp

This is the application for which I originally developed the RP interpreter. The program modifies the R,G,B of each pixel in a color image according to the Reverse Polish expression specified as a command-line argument.

The program reads a color image, filters the image, and creates a new image of the same size as its output. Each pixel is processed individually, independently of the other pixels. For each input pixel, the RP expression is evaluated to compute the R,G,B values of the output pixel from the R,G,B values of the input pixel.
In the RP expression, the variable letters r, g, b are used as both input and output variables. Each of these variables is in the range [0.0, 1.0], where 0.0 means minimum intensity and 1.0 means maximum intensity. The input values of these variables are the R,G,B of the pixel in the input image; and the values of these variables after evaluation of the expression —and then clipped to the range [0.0, 1.0]— are the R,G,B of the pixel in the output image. All other variable letters are local variables.

The format of the input image and of the output image is PPM, more specifically "raw" PPM (magic number "P6").[11] The input PPM image is read from stdin, and the output PPM image is written to stdout.

Below is an example of the use of the fltrppm4 program. It is an experiment for one way to reduce the color information in an image to only two quantities per pixel. In this particular experiment, the color information reduction is achieved by collapsing the G (Green) and B (Blue) channels into one single channel (called C for Cyan), as follows:

C := (1-f_CSel)·g_in + f_CSel·b_in

where g_in and r_in are the G and B values of the input pixel; and where f_CSel is a real-valued parameter in [0.0, 1.0] that selects how the C channel is composed from the input G and B channels. The R channel is left unchanged. The two channels of the reduced-color image are thus R and C.

In the output image, this two-channel color information is then displayed as follows:

r_out := r_in
g_out := f_GOut·r_in + (1-f_GOut)·C
b_out := C

where r_out, g_out, b_out are the R,G,B values of the pixel in the output image; and where f_GOut is a real-valued parameter in [0.0, 1.0] that selects how the output G channel is composed from the two pixel components r_in and C in the reduced-color image. This output transformation of (r_in,C) to (r_out,g_out,b_out) was chosen in this way in order to make to make maximum use of the full output range of all three output channels, and in order so that white remains white. Note that this output transformation is a display aspect only, which does not change the information content of the image.

This color transformation is executed by the following fltrppm4 call:

 ./fltrppm4     \
 	'.3=s; 1s-g* sb* + =c;   .5=t; tr* 1t-c* + =g; c=b'   \
 	< input.ppm   > output.ppm

The variable s is used for the parameter f_CSel (the call above uses the example value 0.3 for this parameter); and the variable t is used for the parameter f_GOut (the call above uses the example value 0.5 for this parameter).
The first two sub-expressions .3=s; 2s-g*sb*+=c; set the s parameter and compute the C channel. The last three sub-expressions .5=t; tr*1t-c*+=g; c=b set the t parameter and compute the output G and B channels. The variable r is left unchanged, so the R channel is copied unchanged from input image to output image.

Example input image:

Example output images:

Note how for f_CSel = 0, the C channel contains the complete G (Green) information of the input, so that the greens remain well differentiated from the skin tones (which are mostly red).
For f_CSel = 1, the C channel contains only the B (Blue) information and none of the G (Green) information of the input; as a result, input frequencies in the yellowish-green range now come through more strongly via the R sensors than via the C channel, so that much of the contrast between red and green disappears. The outputs for f_CSel = 1 may represent how a so-called "color-blind" person probably perceives the world.

Dependencies and build

The source file of each of these three example application programs uses as its external dependencies only the following:

The RPInterpreter library and its external header rpinterpreter.h
The header file llgp_between.h defining my general-purpose macros BETWEEN_Xxx()
The standard C libraries interfaced by <assert.h>, <stdio.h>, <limits.h>, <stdlib.h>, <stdarg.h>, <string.h>, <math.h>, and <fenv.h>. The last one is used for feclearexcept() and fetestexcept(), as explained in the section Floating-point exceptions above.

Building the C++ sourcefile of each of the three example programs into an executable goes as follows (on GNU/Linux):

  g++  -Wall -ggdb  -o APPEXAMPLE  APPEXAMPLE.cpp  rpinterpreter.a  -lm

where APPEXAMPLE.cpp is the name of the application source file.

The links to the source files in the subsections above lead to representations of the source files in the form of HTML pages. A gzip archive that contains the source files for these three example application programs in their original form (and with the original file names) is here. Unpack: gunzip applications.tar.gz, then tar -xvf applications.tar

SEE ALSO

An interpreter for a new BASIC-like script language using functions and local variables, that I developed for a professional assignment.

In that interpreter, I used the same general design lines as the ones sketched in this page. The main difference is that for that project, the data structures for the interpreter state and for the internal representation of the executed code were more complex: each function resulting in a separately stored executable code block; and implementing true local variables by using a local symbol table instance during the execution of a function, for the local variables used inside the function.

NOTES

[1]	Output via via variables only. The reason why I chose the method of output via variables and not the method via return value(s) is that with the output variable method, a simple design suffices to provide great flexibility to application programs. The problem with the output method via return value is that in it, the output is inherently tied to the basic concept of the RP expression itself: If an application needs multiple numeric values passed back to it as the computation result, then (barring use of vector data types) one separate RP expression must be specified for each output value. In contrast, the output method via variables uses a so-called side effect of the evaluation of the expression, which decouples the output from the inherent aspects of the expression. With this, the functionality of returning any number of output values (up to the number of available variable names) can be provided by an interpreter that is fixed to accept only one single expression string.
[2]	The input and output variable names are fixed by the application code. This is completely analogous to how in programming languages like C/C++ and Pascal, the number and the names of the formal function parameters used in the code block of a function are not determined by this this code block, but are hardcoded in the function signature specified above the code block. The RP expression is only the code block, and the "function signature" (function prototype) is fixed by the application code.
[3]	*Casting of the `void ` member variables of `RPInterpreter`.** In general, casting is rightly regarded as not the most elegant of operations, but in this case the casts are very localized (namely to the `RPInterpreter` member function implementations only), and the inelegancy of using casts is outweighed by the isolation that is achieved. A programming language is in my view not Selbstzweck but only a means for the implementation of designs. I think that achieving a clean design (a clean logical structure of the software) is more important than, and takes precedence over, the exact details of how the coding is implemented. In particular, I think that achieving cleanly structured software takes precedence over any idealistically conceived general "coding rules". The above is an example where breaking a general coding rule allows a cleaner code structure.
[4]	*An incidental further effect of using only `void ` member variables in the client-used class** is that after a change in the `RPInterpreter` implementation, the object files of the compiled application code can be linked to the new library without recompilation of the application code. This is a nice effect, but in my view much less important than the hiding of the internal implementation of the `RPInterpreter` class.
[5]	It should be noted very carefully that the combination of words "Floating-Point Exception" is a precise technical term with a precise and special meaning, which is entirely unrelated to the C/C++ exception mechanism (the mechanism that uses the C++ keywords `throw`, `try`, `catch`). In this text, the word "exception" when not further qualified means a C/C++ exception; and the situation of an undefined or unrepresentable result in a floating-point operation is always referred to by the complete term "floating-point exception" or by the abbreviation "FPE", and never by the word "exception" on its own.
[6]	The IEEE 754-2008 standard for floating-point arithmetic. Very awkwardly, the text of this standard is not available for free on the IEEE website, but has to be bought for money (http://standards.ieee.org/findstds/standard/754-2008.html). However, with a little internet-searching a free copy of the text of the standard can of course be found in various places on the internet, such as for example on http://www.csee.umbc.edu/~tsimo1/CMSC455/IEEE-754-2008.pdf.
[7]	The flag used in IEEE 754-2008 default handling is a register or variable inside the floating-point arithmetic unit (whether it is implemented in hardware or in software). It can be cleared and inspected by application code. (In C/C++, this is done via the functions `feclearexcept()` and `fetestexcept()` from `<fenv.h>`.)
[8]	Sequence of arithmetic operations: This assumes that all intermediate results in the sequence are used as inputs to operations that eventually produce the output variables, i.e. that in the sequence no intermediate results are computed that are simply thrown away (e.g. via a variable that is computed but overwritten later in the sequence). When using my RP interpreter, checking for domain errors via the `getVar()` return value does not detect domain errors, during evaluation of the RP expression, in computations of intermediate results that are thrown away and that have no effect on any output variable. (Such FPEs are however still detected by a single simple `feclearexcept()` and `fetestexcept()` pair in the client code bracketing all `evaluate()` calls.)
[9]	The "4" at the end of the names of the test application programs has only historical reasons, and has no significance otherwise. (It is the version number of the image filter application program for which eventually the RP interpreter was later developed.)
[10]	Function plotter application using fixed x and y ranges. I wrote this simple plotting application as an additional way to test some aspects of the RP interpreter more quickly than is possible with the simple test driver `testrp4.cpp`, and also more specifically to test scaling functions (specified as RP expressions) for use in the image filter application `fltrppm4.cpp`. This last goal explains the limitation to the fixed intervals [0.0, 1.0].
[11]	PPM image file format. This is a well-known file format for uncompressed color images. Conversion between PPM and compressed image formats like JPEG and PNG is done by widely available standard programs. (For example, on Linux, `djpeg` or `jpegtopnm` to convert JPEG to PPM, and `cjpeg` to convert PPM to JPEG.)

`a.3* b.7* + =z`	Compute 0.3 a + 0.7 b, and copy the result into the variable `z`.
`.3=f ; fa* 1f-b* + =z`	Set the temporary variable `f` to the value 0.3, and check that the stack is empty. Then compute f·a + (1-f)·b and copy the result into the variable `z`.