http://rubinghsoftware.de/projects/dako_3d/

Page contents Kurzbeschreibung Mathematischer Hintergrund Teilaufgaben     Datenstrukturen     Schnittkurven berechnen         (Analytisch)         (Numerisch)         (Endpunkte)     Tessellator     Regression testing Documentation sample Acknowledgements Zeugnis

Kurzbeschreibung

Für diesen Auftrag habe ich einen neuen 3D-Kern entworfen und implementiert, für Einsatz in Programmen für Computer Aided Design (CAD), in 3D, von mechanischen Bauteilen. 

Die wichtigste Funktion dieses 3D-Kerns ist, eine CSG-Operation zu berechnen (CSG = Constructive Solid Geometry), wobei sowohl die zwei input-Körper als auch der output-Körper repräsentiert werden durch ihre Oberflächensegmente und Kanten; und wobei der output-Körper als input für weitere CSG-Operationen verwendet werden kann. 

Der 3D-Kern wurde strikt isoliert von OpenGL und von jeder visuellen Darstellung. 

Mathematischer Hintergrund

Das Wort "3D-Kern" bezeichnet die Software-Funktionalität (software library) die zuständig ist für die mathematischen Operationen die intern in dem 3D CAD Anwendungsprogramm benötigt werden. 

Die wichtigste Funktion des von mir entwickelten 3D-Kerns ist, eine CSG-Operation auszuführen (zu berechnen).  In dem CAD Anwendungsprogramm wird, wie auch in vielen anderen 3D CAD Programmen, so vorgegangen dass der CAD-Zeichner ein komplexes Bauteil schrittweise zusammenstellt über Constructive Solid Geometry (CSG), das heißt durch das Schneiden, Subtrahieren, und Zusammenfügen von einfachen 3D-Körpern.  Jede einzelne CSG-Operation ist also eine Operation auf 2 Körper, die als Ergebnis ein neues (und komplexeres) Körper produziert; und ist eine der klassischen Mengenoperationen: Schnittmenge (intersection), Differenz (difference), oder Vereinigung (union)[1]. 

Im 3D CAD Programm des Auftraggebers war ursprünglich das vom Zeichner konstruierte 3D Bauteil nur verfügbar als "Rezept" der sukzessive ausgeführten CSG-Operationen.  Ziel meiner Aufgabe war, das konstruierte Bauteil zusätzlich verfügbar zu machen als boundary representation, das heißt als mathematische Spezifikation der Oberfläche des fertig konstruierten 3D Körpers.  Diese boundary representation war notwendig um es dem CAD-Anwendungsprogramm zu ermöglichen, die konstruierten Bauteile abzuspeichern in der Form einiger zusätzlichen vielbenutzten CAD-Dateiformate. 

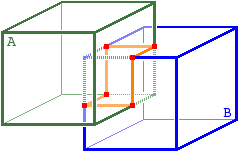
(Abb. 1)   A simple case to show the basics of how an individual CSG operation is performed on the boundary representation level.  The two input solids to the CSG operation are the two cubes A (green) and B (blue).     Shown in orange are the curve segments where the surfaces of the two solids intersect.  The orange curve segments cut up a number of the surface segments of the two solids into parts.  The surface of the output solid of the CSG operation is composed of: (1) a subset of exactly these cut-up surface parts, plus (2) a subset of those input surface segments that were not cut up by the orange curve segments.      Furthermore, for each of the four possible CSG operations (A-B, B-A, A∩B, A∪B), the set of edges of the output solid always contains all of the orange curve segments.

Die boundary representation eines 3D Körpers besteht aus einer Menge von Oberflächensegmenten (surface segments), Kanten (edges), und Eckpunkten (vertices), wobei die Oberflächensegmente eine einfache mathematische Beschreibung haben.  (Für diese Aufgabe waren nur 4 Typen von Oberflächensegmenten benötigt: Ebene, Zylinder, Kegel, und Torus.) 

Mit Verwendung meines neuen 3D-Kerns wird jede CSG-Operation ausgeführt (errechnet) auf der boundary representation Ebene. 
    Aufgabe meines 3D-Kerns ist also, gegeben eine auszuführende CSG-Operation (intersection/difference/union), und gegeben die boundary representation der zwei input-Körper der CSG-Operation, dann daraus die boundary representation zu berechnen des output-Körpers dieser CSG-Operation.  Der so berechnete output-Körper einer CSG-Operation (in der Form seiner boundary representation) wird dann benutzt als input-Körper für die nächste CSG-Operation. 

Teilaufgaben

Datenstrukturen

Eine der (einfacheren) Teilaufgaben ist selbstverständlich gewesen das Entwerfen der Datenstrukturen benötigt für die boundary representation eines 3D-Körpers.

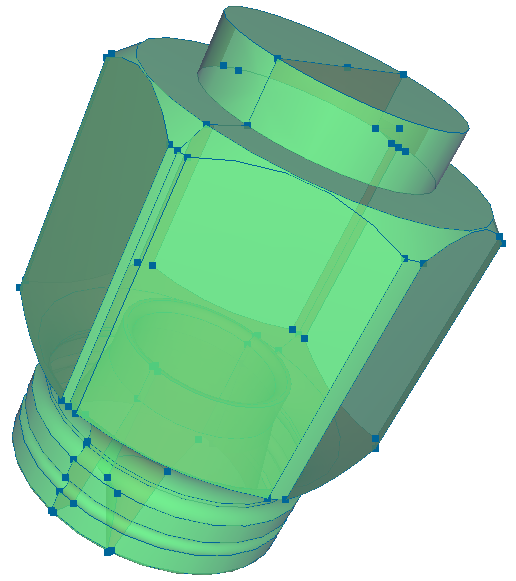
(Abb. 2)   As is usual in 3D computer graphics, each surface segment in my 3D kernel is represented as a parameterized surface (x,y,z) = P(α,β), bounded by closed loops of curve segments.  Similarly, each curve segment (edge) is represented as a parameterized curve (x,y,z) = P(α), bounded by two vertices.      Each curve segment handled by the 3D kernel is always part of at least one surface segment (ConS, Curve on Surface), namely it is usually a curve on two different surface segments simultaneously.

Die wichtigsten Datenstrukturen, bereitgestellt von der 3D-Kern library an die Anwendungssoftware, und intern verwendet innerhalb des 3D-Kerns, sind gewesen:

• Eine Klasse die einen gesamten 3D-Körper enthält in boundary representation (intern repräsentiert als zusammenhangende Menge von Oberflächensegmenten, Kanten, und Vertices)
• Eine Klasse für ein beliebiges Oberflächensegment, implementiert als virtual base class für die 4 möglichen Typen von Oberfächensegmenten
• Eine Klasse für ein beliebiges Kurvensegment (Kante, edge), implementiert als virtual base class für alle möglichen Typen von Kurvensegmenten (inklusive die numerisch berecheten Schnittkurvensegmente)
• Und schließlich, trivialerweise, eine Klasse für ein Eckpunkt (vertex).

Die dem CAD-Zeichner verfügbaren atomischen Körper haben sich in dieser Aufgabe beschränkt auf Körper die erzeugbar sind durch Extrusion oder Rotation einer ebenen Kontur bestehend aus Geradensegmenten und Kreissegmenten.  Daher waren für diese Aufgabe nur 4 Typen von Oberflächensegmenten benötigt: Ebene (Extrusion von Gerade), Zylinder (Extrusion von Kreis), Kegel (Rotation von Ebene), und Torus (Rotation von Kreis).  Durch eine CSG-Operation können nur neue Typen von Kanten (Schnittkurven) entstehen, aber nicht neue Typen von Oberflächen. 

Schnittkurven berechnen

Die wichtigste Teilaufgabe beim errechnen einer CSG-Operation auf der boundary representation Ebene ist, die Schnittkurven zu berechnen von zwei Oberflächensegmenten. 
    "Schnittkurven zu berechnen" bedeutet, genauer formuliert, dass die Kurven-Segmente gefunden werden wo die Oberflächensegmente der beiden input-Körper der CSG-Operation einander schneiden.  Diese Schnittkurvensegmente (orange im Diagramm unten) bilden Kanten (edges) im output-Körper der CSG-Operation. 
    Die Schnittkurvensegmente müssen —wie auch jede andere Kante in der boundary representation eines Körpers— als parameterisierte Kurven repräsentiert werden.  Ziel der Schnittkurvenfindung ist also, Parametergleichungen zu finden für die Schnittkurvensegmente. 

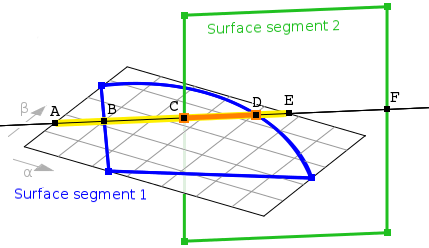
(Abb. 3)   Overview of the basic geometrical situation when intersecting two surface segments.      Each of the two intersected surface segments is bounded by a contour (blue, green).      The intersection of the two surface segments is the bounded curve segment CD (orange).  This is a segment of the (unbounded) intersection curve between the two (unbounded) surfaces, namely it is the segment of the (unbounded) intersection curve that falls within the contours of both of the surface segments.

Die Schnittkurven wurden im 3D-Kern analytisch berechnet wo möglich, und numerisch für komplexere Fälle.  Der numerische Berechnungsweg ist für alle Oberflächentypen verwendbar.  Für die einfacheren Fälle wurde der analytische Berechnungsweg aber bevorzugt wegen seiner unschlagbar schnellen Laufzeit. 

Schnittkurven berechnen — Analytisch

Wenn die zwei sich schneidenden Oberflächensegmenten von einfacher Art sind (z.B. Ebene + Ebene, oder Ebene + Zylinder), dann ist es einfach, analytisch die Parametergleichung für die Schnittkurven zu finden. 
    (Nämlich: Substutution der Parametergleichung für eine der Oberflächen (x,y,z) = P(α,β) in die implizite Gleichung der anderen Oberfläche f(x,y,z) = 0, dann Lösung so dass eine Formel entsteht für Parameter β als Funktion von α, und schließlich Zurücksubstitution dieser Formel für β in die Parametergleichung für die erste Oberfläche, ergibt die Parametergleichung für die Schnittkurve (x,y,z) = P(α).)

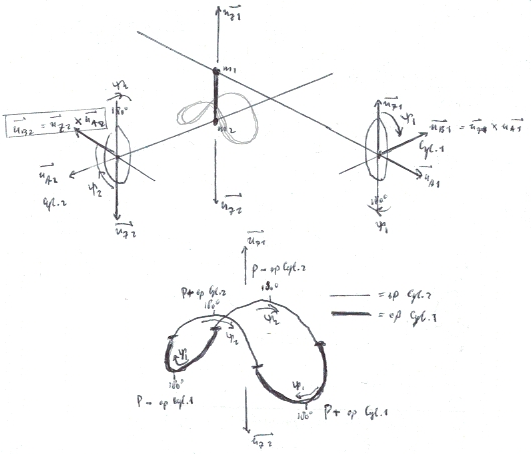
(Abb. 4)   The basic layout of a relatively complex case of intersection curves computed analytically: the intersection curves between two cylindrical surfaces.      The upper sketch shows the axes of the two cylinders.  The lower sketch shows the intersection curve segments, and the parameter by which each of these intersection curve segments is parameterized.

Dieser analytische Lösungsweg ist aber unmöglich wenn die sich schneidenden Oberflächen beide von einem komplexen Typ sind.  In diesem Fall wird nämlich der Polynom-Grad der zu lösenden Gleichung für Parameter β zu hoch dafür, im Allgemeinfall noch analytisch lösbar zu sein.  (Zum Beispiel: Schneiden von zwei Torus-Oberflächen ergibt im Allgemeinfall eine Gleichung 8. Grades in den Parametern α und β.)

Schnittkurven berechnen — Numerisch

Ein numerisch gefundenes Schnittkurvensegment wird intern repräsentiert durch eine geordnete Liste von Punkten auf dem Kurvensegment (Stützpunkten).[2] 
    Die zwei Teilprobleme beim numerisch Finden der Schnittkurven zweier Oberflächensegmente sind: Finden einer Menge von Punkten die zu den Schnittkurven gehören, und Zuordnung (Sammeln) dieser Punkte zu zusammenhangenden Kurvensegmenten.

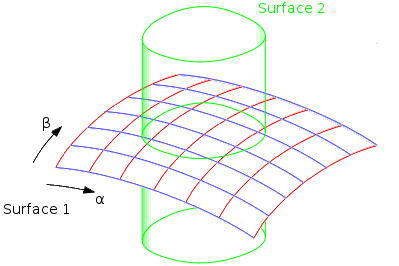
(Abb. 5)   Das Finden einer Menge von Punkten auf den Schnittkurven wird wie folgt gemacht.      Es wird wieder die Parametergleichung (x,y,z) = P1(α,β) benutzt für eine der Oberflächen (Oberfläche 1), und die implizite Gleichung f2(x,y,z) = 0 für die andere Oberfläche (Oberfläche 2).      Die Grundidee des Lösungsweges ist, uns über Oberflächensegment 1 zu bewegen entlang einer Kurve (grid curve) mit α = konstant und mit β = variabel (rot).  Entlang einer solchen grid curve betrachten wir die Funktion f2(x,y,z) = f2(P1(β)) = f2(β).  Die Nullstellen dieser Funktion sind die Punkte wo diese grid curve die Oberfläche 2 schneidet.  Damit ist dieses Teilproblem reduziert zum Finden der Nullstellen einer Funktion von einer Variablen, ein bekanntes Problem in der numerischen Mathematik.  Im 3D-Kern werden die Nullstellen dieser einvariablingen Funktion gefunden durch zunächst eine grobe Ortung der Nullstellen über einen intelligent gesteuerten Einsatz der bisection method, gefolgt für jede einzelne Nullstelle durch eine Verfeinerung über einige Newton-Raphson-Schritte.      Selbstverständich kann das gleiche gemacht werden für grid curves auf Oberflächensegment 1 mit α = variabel und mit β = konstant (blau), d.h. in dem Fall Finden wir die Nullstellen der Funktion f2(x,y,z) = f2(P1(α)) = f2(α).

Das erste Teilproblem wird gelöst dadurch dass auf eines der sich schneidenden Oberflächensegmente eine Menge grid curves mit α=konstant (rot), und separat auch eine Menge grid curves mit β=konstant (blau), geschnitten werden mit dem anderen Oberflächensegment, wie beschrieben beim Diagramm oben.  Hiermit ist est sichergestellt dass wir genug Punkte finden die zu den Schnittkurven der zwei Oberflächensegmente gehören (je feiner das α,β-Grid, desto genauer die numerischen Schnittkurven). 

Die Zuordnung der so gefundenen Punkte zu zusammenhangenden Kurvensegmenten ist ein separates Problem (wofür das bekannte mathematische Standardrepertoire keine Bausteine anbietet).  Für dieses neue Problem habe ich einen (nicht-iterativen) Algorithmus entwickelt basiert auf der Vorgehensweise grob beschrieben bei folgendem Diagramm. 

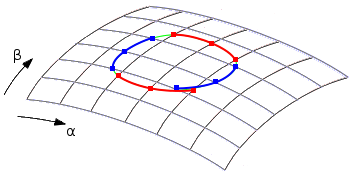
(Abb. 6)   Der Algorithmus sammelt zunächst die gesamte Menge 3D-Punkte auf den Nullstellen der grid curves mit α=konstant zusammen zu einer Menge vorerst noch separater Teilkurven (Teile der zu findenden gesamten Schnittkurven), die "constant-α-Teilkurven" (rot).  Danach werden analog die Menge 3D-Punkte auf den Nullstellen der grid curves mit β=konstant zusammengesammelt zu einer Menge von "constant-β-Teilkurven" (blau).      Durch Hinzufügen von zusätzlichen grid curves (die regulär numerisch verarbeitet werden) auf die Endpunkte dieser Teilkurven wird sichergestellt dass diese Teilkurven zwischen einander auf eindeutige weise überlappen.  Letzteres erlaubt es dann schließlich, die Teilkurven zusammenzunehmen zu kompletten Kurvensegmenten.

Schnittkurven berechnen — Endpunkte

Beide Berechnungswege (analytisch und numerisch) ergeben zunächst die Schnittkurven in der Form von Kurvensegmenten die nur begrenzt werden durch die Grenzen der Oberflächenparameter α,β eines der zwei geschnittenen Oberflächen (gelbes Kurvensegment AE in Abb. 3). 
    Als letzter Schritt ist er daher immer notwendig, diese noch zu langen gelben Kurvensegmente zu schneiden mit den Konturen der beiden Oberflächensegmente (blau und grün in Abb. 3), damit die Endpunkte gefunden werden der gesuchten Schnittkurvensegmente (orangenes Kurvensegment CD in Abb. 3). 

Zwei durch digitale Berechnung entstandene Kurven in 3D schneiden sich natürlich generell nie 100% exakt.  Die Software findet daher genaugenommen nicht Schnittpunkte, sondern findet die Punkte auf den zwei Kurven die die kleinste Distanz zwischen sich haben. Zum Finden dieser Punkte wurde die geometrische Idee hinter der Newton-Raphson Methode benutzt, wie beschrieben beim folgenden Diagramm. 

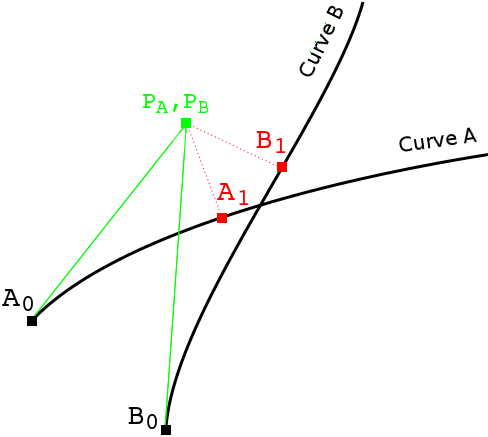
(Abb. 7)   Iterative algorithm to find the points on two 3D curves that are nearest to each other.  Note that the diagram depicts a situation in 3D, not in 2D.      A0 and B0 are initial points on curves A and B, respectively.  Take the lines tangent to the curves at these points, and compute the points on these two tangent lines that are nearest to each other; call these points PA (on the tangent line through A0), and PB (on the tangent line through B0).  Invert PA to curve A, i.e. compute the point on curve A nearest to point PA; call this point A1.  Similarly, invert PB to curve B, yielding point B1.      A1 and B1 are nearer to the closest points on the two curves than A0 and B0 were, and replace these initial points A0 and B0.  Repeat the same step until sufficiently accurate convergence is reached for the two points A0 and B0.

Zwei beliebige Kurvensegmente können natürlich im Allgemeinen mehr als nur 1 Schnittpunkt haben.  Zum Finden aller Schnittpunkte (aller Stellen wo die zwei Kurven sich nah annähern) wurde Rekursion eingesetzt, nämlich nach Finden eines Schnittpunktes werden die Kurven dort zerteilt, wonach dann die separaten Teile miteinander geschnitten werden (und so weiter bis keine weiteren Schnittpunkte gefunden). 
    Dass dieses Verfahren alle Schnittpunkte findet konnte sichergestellt werden dadurch dass für komplexe Kurvensegmente mehr als nur ein Paar von strategisch positionierten initiellen Punkten A₀,B₀ ausprobiert wird (der Komplexitätsgrad der zwei geschnittenen Kurvensegmente ist bekannt). 

Tessellator

Als Teil des Projektes wurde einen Tessellator entwickelt der einsetzbar ist für gebogene (d.h. nicht-ebene) Oberflächen.  Dies war notwendig weil, werkwürdigerweise, keiner der eingebauten Tessellatoren in den verfügbaren OpenGL libraries in der Lage war, nicht-ebene Oberflächen zu tessellieren. 

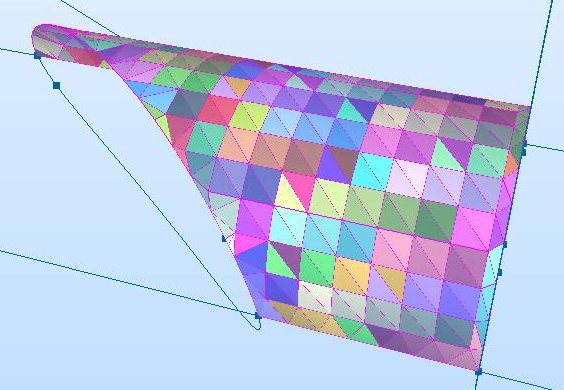
(Abb. 8)   The tessellation of a non-planar surface segment (here: a cylinder surface segment).      Typical 3D graphical display libraries, such as OpenGL, are designed and optimized for drawing planar 3D surface elements bounded by contours composed of a few straight-line segments.  Therefore, to display a surface segment that is curved and/or that has a complex boundary, it must be represented, during drawing, as a set of small, planar surface elements (its tessellation).      Note that the tessellation of a surface segment is strictly only a part of the visual representation process; and has nothing to do with the boundary representation of the solid (as a set of surface segments, edges, and vertices) that is operated upon during the computation of a CSG operation.

Regression testing

Wie üblich in nicht-trivialen Softwareprojekten, wurde auch im 3D-Kern eine Funktionalität hinzugefügt zum regression testing, plus eine Menge Testfälle.  Für den 3D-Kern war dieses regression testing absolut unerlässlich, nicht nur wegen der Komplexität der Software, aber auch wegen der großen Menge der mathematischen Spezialfälle. 
    Diese Spezialfälle treten auf wenn zwei Oberflächensegmente teilweise zusammenfallen, oder wenn zwei Oberflächensegmente einander schneiden nicht in einer Kurve sondern in einem Punkt (z.B.: Ebene wird nur in einem Punkt berührt von Torus-Oberfäche, oder Ebene wird berührt von nur einem Punkt in der Grenzkurve eines Oberflächensegments).  Solches Zusammenfallen passiert in der Praxis oft, weil beim 3D CAD Zeichnen oft absichtlich so konstruiert wird.  Das Zusammenfallen wurde überall im 3D-Kern überprüft und detektiert aufgrund eines vorgegebenen Distanz-Schwellenwertes (Konstruktionsgenauigkeit). 

(Abb. 9)   A small extract from the input file to the regression tester, specifying the test cases to be executed.  This extract contains only three of the 135 test cases used in total.     For each test case, a file is loaded containing the specification of a number of solids (WF), and then a number of 3D kernel operations are executed (CS).  After this, the number of surface segments in the result solid (IS) is compared with the expected number of surface segments (NM).      The number of surface segments in the result solid is extremely sensitive to any type of error in the CSG operation, and this test criterion was not only simple to specify but also proved to be very reliable for catching errors.

Documentation sample

In allen Softwareentwicklungs-Projekten versuche ich, neben Dokumentation über die in der Software benutzen Algorithmen, im Sourceverzeichnis immer eine Textfile aufzunehmen die eine kurze Übersicht gibt über die Sourcefiles.  Die entsprechende für dieses Projekt abgelieferte Textfile ist hier.
    Die Textfile gibt eine Auflistung aller Sourcefiles, beschreibt kurz den Zweck jeder Sourcefile, und legt vor allem dar, wie die Zusammenhänge (dependencies) zwischen den Sourcefiles strukturiert sind.  Zweck dieser Sourcen-Übersicht ist, den nächsten Programmierern die nach mir den Code anfassen, den Zugang zu den Sourcen zu erleichtern. 

Acknowledgements

Dank gebührt dem technischen Leiter der DAKO CAD-Softwareabteilung, Volker Scheffer, für die gute Zusammenarbeit; dem damaligen Mitarbeiter Alex Lärz für den nützlichen fachlichen Gedankenaustausch; und der DAKO-Geschäftsführung, für die Vergabe dieser interessanten Aufgabe! 

Zeugnis

Ein Arbeitszeugnis des Auftraggebers kann ich Ihnen auf Anfrage gern senden.

Anmerkungen